What would be the impact on Malaysia of a recession in Europe? To look at this question, I’ve come up with a few equations.
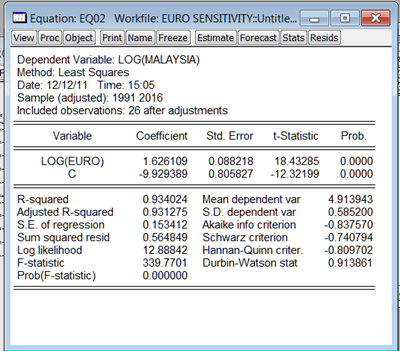
First a single equation approach, taking just Malaysia and Europe. I’m using the annual GDP numbers from the IMF’s September 2011 World Economic Outlook database (available here), transformed into logs to translate the results into elasticities, with the following results:
The relationship is statistically significant, and suggests that a 1% increase (decrease) in Eurozone GDP would result in a 1.62% increase (decrease) in Malaysian GDP. Based on this, Malaysia has a high degree of sensitivity to European growth.
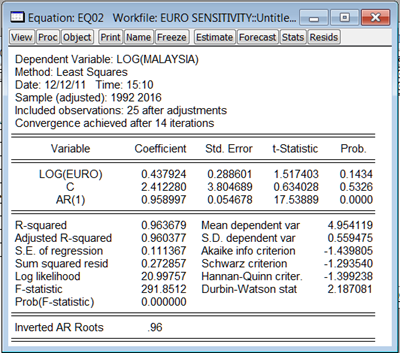
There’s a problem though – residual tests show a high degree of serial correlation. Re-specifying the equation with a one lag autoregressive term (as suggested by looking at the correlogram) to handle the serial correlation, we get the following:
The p-value has now risen from zero to 0.1434 – which means the Euro coefficient is no longer statistically significant at the 95% level or even the 90% level. The estimate of the coefficient has also fallen by nearly three-quarters, to 0.438, suggesting Malaysia’s GDP only moves by 0.4% for every 1% movement in Euro GDP.
Taking another approach (also within a single equation framework) I took the GDP record of Malaysia’s top five trading partners, as well as the residual GDP for the rest of the world (all data from the same source) using the following specification:
Log(Malaysia) = α + Log(US) + Log(Europe) + Log(China) + Log(Singapore) + Log(Japan) + Log(ROW) + ε
The results (sample range 1991-2016):
Only Singapore tests out as statistically significant at the 95% confidence interval – Europe is within 86%, and the rest are even worse. In short, you cannot discount that a recession in Europe would have no effect on Malaysia at all.
Assuming it does though, and that the coefficient is unbiased, then a 1.0% drop in European GDP would cause Malaysian GDP to drop just 0.3%. A European recession which shaves off 3% from European GDP would cause Malaysian GDP to drop just 1%, which would be bad, but not disastrous.
The problem with single equation estimates is that when you’re looking at global economies this way, they are all inter-related. So it would be more theoretically correct to try and do a simultaneous equation approach or a VAR, where these relationships are explicitly taken into account in the regression estimates.
Here’s the results from a VAR (quoting just the results for Malaysia), using two lags:
Log(Malaysia) = 0.28*Log(ROW(-1)) + 0.16*Log(ROW(-2)) - 2.67*Log(US(-1)) + 3.10*Log(US(-2)) + 0.88*Log(Euro(-1)) - 0.228*Log(Euro(-2)) - 0.03*Log(Japan(-1)) + 1.14*Log(Japan(-2)) - 0.04*Log(China(-1)) + 0.36*Log(China(-2)) + 0.68*Log(Singapore(-1)) - 0.95*Log(Singapore(-2)) - 0.38*Log(Malaysia(-1)) - 0.36*Log(Malaysia(-2)) - 16.11
I’m cheating a bit here – cointegration tests show multiple cointegration relationships that just about equal the number of regressors. That means the best approach is to use an unrestricted VAR in first differences. I’ve foregone that particular problem by just going ahead with levels, which are a lot easier to interpret.
The only two regressors that are significant are Japan at two lags and Singapore’s (also at two lags) though the latter is borderline. Europe is again not statistically significant, and the signs of the coefficients of the two different lags are opposing. The first lag shows a large impact of 0.88, but the opposite sign of the second lag suggests that the impact is short lived.
Moving on to the variance decomposition (click on the pic for a larger version):
…no more than 12% of the variance in Malaysia’s GDP is explained by changes in Europe’s GDP. Most of the changes in Malaysia’s GDP trend is explained by global GDP as a whole, rather than specific countries – US, Europe and Japan collectively explain no more than 30% of the variance in Malaysia’s GDP. Bear in mind that doesn’t refer to GDP itself, but fluctuations in GDP.
Based on the foregoing, it looks like a near term Eurozone recession, where annual GDP growth drops between 1%-2%, would at worse shave off perhaps 0.7%-1.4% from Malaysia’s trend growth rate.
If we’re looking at a baseline scenario for 2012 of 5%-6% GDP growth in Malaysia, then the impact of a Eurozone recession might reduce growth to 3.5%-4.5% as the worse case outlook. In all likelihood, the impact would probably be far less.






Hishamh,
ReplyDeleteI think that the cointegration tests do matter. For example, a 1-2% drop in Eurozone GDP will also cause a drop in the US GDP, Singapore GDP etc. as you have pointed out. In particular, your tests running log(Malaysia) vs a whole bunch of countries would suffer from multicollinearity, which would jack up the standard errors, causing some of the countries to be less significant than they appear.
Another thing to note is that, what you have concluded is only the effect of a drop in Eurozone GDP, ceteris paribus. I think what would happen is that all the other countries that you mentioned would suffer a drop in GDP as well. Let's just assume that the coefficients that you tested are correct, and each of the other countries would suffer a 1-2% drop in GDP, Malaysia's GDP growth would be far far less than what you have concluded. In my opinion, you may have underestimated the impact, rather than overestimated.
My statistics is a bit rusty, perhaps I missed something somewhere?
Main Streeter,
ReplyDeleteI didn't say the cointegration tests didn't matter - I said the number of cointegration vectors equaled the number of variables. In plain English, everything affects everything else, basically proving your point regarding multicollinearity.
Hence the estimates I used in the conclusion were based on the VAR, not the single equation estimates where multicollinearity would be a significant problem. The VAR structure, where all variables are treated symmetrically as endogenous and estimated concurrently, takes care of that.
It only looks like a single equation estimate because I only quoted the relevant estimates for Malaysia, rather the whole VAR system itself (which would be a little difficult to squeeze into a blog post).
But if you have cointegrating vectors equal in number to your endogenous variables, the system reduces to a VAR in first differences - you can't estimate a VECM. That's where I cheated, because a VAR in first differences is a little hard to interpret - you're talking about acceleration or deceleration, rather than the rate of change.
In any case, the results for a VAR based on first differences doesn't differ much from the VAR based on levels - it's still Japan and Singapore at two lags, and the estimates for Europe remain statistically insignificant.
I really ought to try this with quarterly data, but they will have to wait until I can get a source.
Hishamh
ReplyDeleteActually you can get quarterly data from IMF. You can sign up for a 5-day free trial for the IMF-IFS statistics. They have quarterly data back until 1980 I think.
Only thing is that it is a 5-day trial. So you can't update it in the future. But of course, you can always sign up for a new email and re-sign up for a new 5-day trial. Here is the link:
http://elibrary-data.imf.org/
In the meantime, I will go brush up on VAR. Thanks!!
Yeah I know about IFS - I used it for my master's thesis, but that was a few years back (downloaded the whole thing in 3 days!). I'd rather something that was freely publicly available, so everyone can go in and check for themselves.
ReplyDeleteHave fun with VARs! Sims got his Nobel prize this year for advocating them.