Testing The Purchasing Power Of Gold

[This post has been a few days in gestation, because I had to deal with my laptop finally dying on me after six years of heavy duty wear and tear– RIP Thinkpad – and the sheer amount of work collating and analysing the data. Hope you guys enjoy this.]

I’ve been following the arguments on rocky’s bru blog on whether the introduction of the dinar and dirham in Kelantan was a good idea. This is of course a completely separate issue to whether Kelantan is within the law in doing so.

But the arguments in support seem to devolve along the following four lines:

1. Gold and silver were used as the basis for currencies during much of Islamic history, and thus for that reason worthy of emulation;
2. Gold and silver are less susceptible to speculation;
3. The value of gold and silver to other commodities are more stable relative to fiat currencies;
4. They also maintain their value better against other commodities over time.

The first argument is indisputable, while the second is absolutely untrue – the present bull run in gold is about as frothy a bubble as I’ve ever seen. The other two arguments sound similar, but actually aren’t. Argument 3 is a hypothesis regarding the variance of commodity prices in gold terms relative to fiat currencies; argument 4 is a hypothesis of the mean –both can be statistically tested.

I originally intended this post to test hypothesis 3 and 4, but as it turns out I needn’t have bothered – all you need is an eyeball check.

So lets say you have a set of commodity time series priced in US dollars. You can get the prices of these commodities in gold terms by dividing the US dollar prices with the gold price in US dollars.

The approach to testing for gold maintaining its value against other commodities is fairly trivial in statistical terms, which involves answering the question: is the commodity price in gold terms a stationary series? In other words, we need to test whether the mean is constant over time (mathematically, testing whether the series has a unit root).

The data set I’m using comes from the IMF covering a wide variety of commodities, while gold prices are from the Bundesbank’s database (H/T wy – thanks!), using the London Metal Exchange morning fix prices. The sample range is from January 1980 to July 2010, in monthly frequencies.

I was expecting even before starting that I’d be able to prove that gold does indeed hold its value against other commodities and in fact should slightly increase in value, and that the volatility would be lower than the USD price of the same commodities.

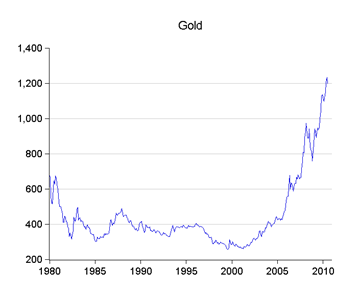
Disclaimer: I’ve done these tests before on a different dataset (with a lower data frequency), so I was reasonably sure what to expect with respect to stationarity. So imagine my surprise when I didn’t find what I was expecting – but I’m getting ahead of myself. First, the price of gold in US dollar terms:

Gold has been on a declining trend (despite inflation) from 1980 to about 2001, before starting on the bull run we’re seeing today. But it really took off around 2007, when the present financial crisis began to manifest itself.

The argument is that with the amount of monetary stimulus being pumped into the global economy, inflation is bound to increase substantially, which has driven investor interest in gold – never mind that most of the evidence is pointing to the world being subject to continued deflationary pressure for the foreseeable future. But I digress.

Now I can’t show all the commodities I’ve got data for, nor can I fully test them all in the limited time I have – that would take a couple of weeks, and I want to get this post out in a more or less timely fashion. So I’m going to concentrate on the composite indexes instead as representative of commodity movements in gold terms.

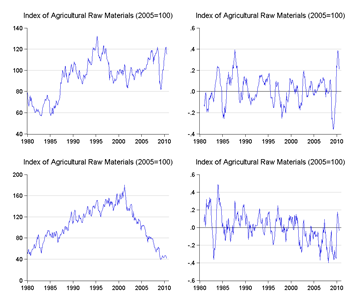
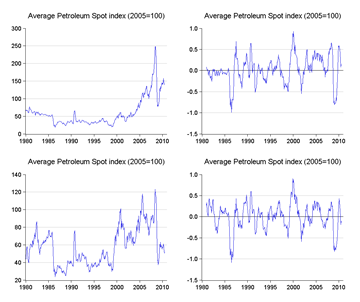
Charts for the selected indexes are presented below in the following format – top row is in US dollars terms; bottom row is in gold troy ounces; left column is index numbers (2005=100); while right column is the annual rate of change in prices in log terms – essentially showing inflation (up) or deflation (down). Got that? :)

So here we go (click on the pics for larger versions):

Looking at the left columns, you’ll see I hit an immediate snag. Except for the metals, industrial inputs and oil indexes, there are fairly obvious trends in the gold price of commodities – it’s subject to inflation up to about 2000, and deflation thereafter.

In other words I cannot by rights do a full sample test for these indexes (because we have a glaringly obvious structural break in the index series); but if I do partial sample tests instead, then the statistical tests for stationarity will almost certainly fail.

Which leads to the conclusion that gold does not in fact hold its value against other commodities over time, except against oil and other metals (I’m 50-50 over industrial inputs).

What was also surprising is that the standard deviations in the log change of the gold price of  commodities was generally higher than the US price – in other words, volatility (and thus risk) was also higher for gold, sometimes startlingly so.

Now it is possible that my sample range is simply too short, as with a sufficiently long sample, some cyclical pattern in prices might emerge i.e. stationarity might emerge. But I don’t have the data sources for that (I’ve been keeping my eye out for some time).

In the meantime, the evidence suggests that the only argument in favour of gold and silver is really a religious argument, as the other three factors don’t appear to be true at the present time.

I’ve always felt that the welfare costs of being chained to a metallic monetary system far outweighed any nominal stability in prices it might bring. Now that nominal stability is looking pretty illusory as well.

Technical Notes

1. Commodity prices and indexes from the International Monetary Fund
2. Gold prices from the Deustche Bundesbank