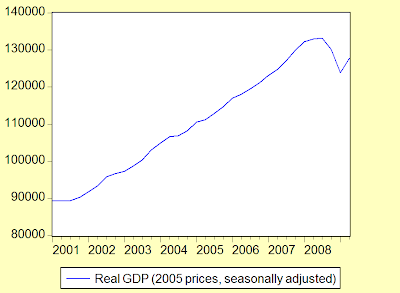
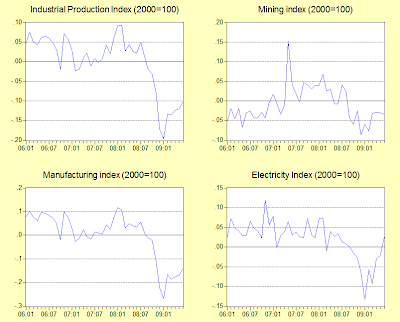
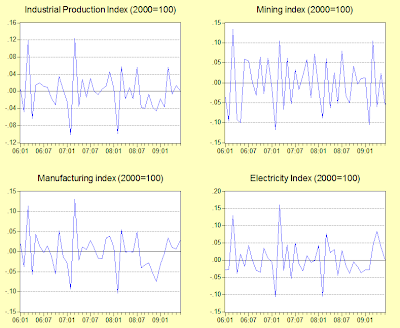
As covered in my previous post, q-o-q GDP rebounded nicely in 2Q 2009 (seasonally adjusted log quarterly changes, annualized, and log annual changes; 2005=100):
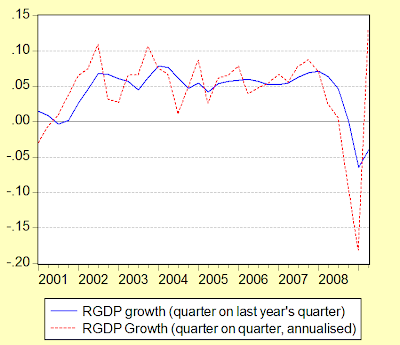
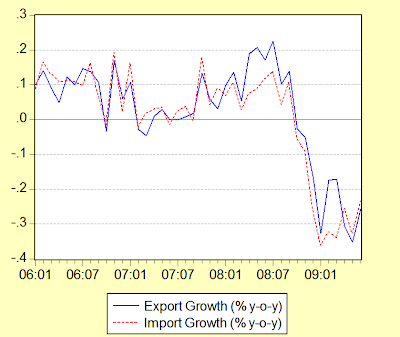
But growth calculations can be misleading – y-o-y is still negative, and for some sectors sharply so, while the q-o-q numbers can be highly volatile. In this instance, I’m more inclined to look at the seasonally adjusted levels, partly to gauge whether the recovery in economic activity is significant, as well as to check on the current level relative to pre-crisis levels. That gives an idea of how much further economic activity has to recover before we can call the economy truly healed i.e. whether we’ve closed the output gap. But first, growth trends on the demand side (seasonally adjusted log quarterly changes, annualized; 2005=100):
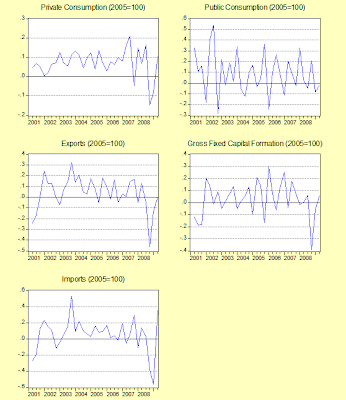
Exports are flat, while private consumption, imports and investment are showing improvement. On to the levels (seasonally adjusted; 2005 prices):
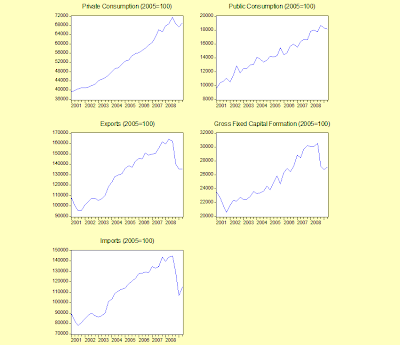
I think we can call the green shoots here as real, but they are very, very small. One thing to note (I just noticed this while compiling these charts), is that private consumption appears to have been above its long term trend in 2007-2008. That suggests that private consumption growth will fall back in the coming quarters, and can’t be relied upon to drive recovery.
There’s one further demand side number that needs to be highlighted. 2Q GDP rose by RM5.9 billion in real terms compared to 1Q, and about RM3.9 billion after seasonal adjustment. Looking at the marginal contribution (seasonally adjusted) from each demand component, we find the external sector (exports less imports) at –RM9 billion, Public consumption –RM1 billion, private consumption +RM1.8 billion, and investment +RM0.4 billion. That means there’s about an RM12 billion discrepancy between consolidated real expenditure and GDP – and it comes from changes in inventories:
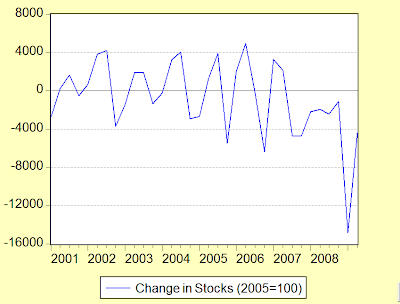
Here’s what I think happened: In response to the drastic drop in trade beginning in 4Q 2008, manufacturers and exporters savagely cut into their ready stock of finished goods, as well as their on-hand supplies of intermediate goods. This hypothesis accords with anecdotal evidence of work stoppages and reduced capacity utilization in 1Q 2009. As it became clear that the global economy was beginning to recover (and as trade finance began flowing again), this trend reversed causing an increase in output to replenish depleted stocks – which fits with the observation of faster import growth but stagnant export growth. Inventories are still dropping however, which suggests that inventory build-up will continue into 3Q 2009 and possibly 4Q 2009. However, here are the key points:
1. External demand for Malaysian goods continues to be stagnant, in line with the observed meagre improvement in monthly export data.
2. That means, in the absence of a pick-up in exports in 3Q, that once inventories are up to more “normal” levels, output will drop again to the level determined by demand.
3. Ergo, recovery will continue to be weak, with a risk of a further dip if neither external demand or domestic demand improve.
It’s also interesting to speculate on the impact of the government’s stimulus packages. One thing to note here is that public consumption under the national accounts is not synonymous with fiscal deficit spending: to see the impact of the latter we need to know what proportion of investment is being done by the public sector, as well as the higher order impact of increased government expenditure on private consumption and investment. Unfortunately, speculate is all we can do at the moment – but I’m inclined to believe that there has been an impact, and that the impact has been greater than the nominal excess in fiscal expenditure i.e. the multiplier is/was greater than one.
I can’t make that argument for the growth in private consumption – that may have been driven more by psychological factors (a return of Keynes’ “animal spirits”) as much as anything else. As news over the second quarter suggested that the worse was behind us, people may have been more inclined to spend – it was not necessarily due to direct or indirect government action. But in terms of investment, I find it hard to believe that the private sector would maintain much less increase investment in an environment of stagnant external demand and very low capacity utilization – especially since the manufacturing sector appears to have begun the recession with excess capacity in the first place.
Whatever the case may be, it’s clear that the main story here is that the bounce in 2Q GDP was largely inventory driven – which is not sustainable. Which in turn means that fiscal deficit spending will have to continue to play a role in sustaining economic activity until external demand recovers, or until new sources of growth are found. That’s a tall order, as I don’t think the external demand situation will improve much going forward – China’s stimulus is already running out of steam, and the US is in no state (nor has the desire) to regain its position as global consumer of last resort.
We live in interesting times.