Today’s industrial production numbers were a pleasant surprise (log annual and monthly changes; seasonally adjusted; 2000=100):
The overall IPI was up 3.0% in annual log terms and 1.5% on the month – not bad numbers by any means, and stronger than I thought it would be, especially after November’s weak output. The report showed upward revisions for November as well, pointing to some momentum entering the new year.
Of course, some of this might just be production brought forward before CNY – in fact, this is quite likely, suggesting a fall back in output for January.
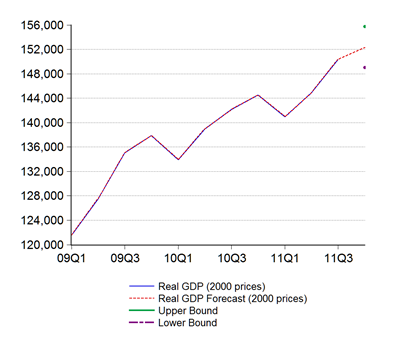
Nevertheless, we’ve got a much rosier picture of 4Q GDP, which is due to be released next week. On the basis of today’s numbers, my GDP forecast just went up from 5.0% to 5.4% (annual percentage) (RM billions; 2000 prices):
That implies full year growth will come in at around 5.2%, a little on the low side from the government’s forecast from 2010, but not bad considering the tribulations the world economy went through in 2011.
Technical Notes:
December 2011 Industrial Production Report from the Department of Statistics






I've always wondered abt this - when you say 'log terms', are you talking about the logarithmic scale?
ReplyDeleteTo be precise, it's in natural logs.
ReplyDeleteThere's two accepted ways to calculate the slope of a line:
1: (x/y-1)*100 gives the normal arithmetic change in percent terms
2: [Ln(x/y)]*100 = [Ln(x)-Ln(y)]*100 gives the logarithmic change
Both are valid but give slightly different answers, though for small changes in slope they're almost the same. You'll notice my figures tend to be a little different from the official figures because of my use of natural logs, but there are some advantages.
For one, it makes life a little easier for calculating things like elasticities, and second, a natural log change is level independent i.e. it doesn't matter what the actual values of x and y are.
It helps that many (un-transformed) economic time series tend to be best fitted with an exponential curve, which means a natural log transformation converts them to a more or less straight line.
It helps that many economic time series tend to be best fitted with an exponential curve, which means a natural log transformation converts them to a more or less straight line.
ReplyDelete