Economists do forecasts – or at least, people think economists have some kind of competitive advantage in forecasting economic variables. But the fact of the matter is, most economists have only a passing familiarity with forecasting and all that goes into it.
The reason why economists, and especially financial market economists, do forecasts is pretty disappointingly prosaic, and the essence of which can be captured by this joke:
“Economists don't answer to questions others make because they know what the answer is. They answer because they are asked."
We’re asked to give forecasts, because it’s presumed we know what’s likely to happen – but that’s based on the presumption that an expert on economics is also an expert in forecasting. But those are two very different fields.
In fact, ask an economic theorist about forecasting, and you ‘re likely to get a reply similar to Nick Rowe’s:
How is model-based macroeconomic forecasting possible?
I can figure out how some things work. I can't figure out how other things work. But there are some things I can't figure out how it's even possible for them to work. Using macroeconomic models to make macroeconomic forecasts falls into that third category of things. I can't see how it's even possible to do it. And yet people claim to do it all the time...
...This is really simple stuff. Either I'm making some awfully simple mistake, or all the people who claim to be making model-based macroeconomic forecasts are just blowing smoke. They must have thought about this problem. I'm laying bare my ignorance (I never claimed to know much econometrics anyway). Someone's got to ask this stupid question; it might as well be me.
Start with a structural model. It has a system of equations S. Each equation relates one endogenous variable y to other endogenous variables Y, and exogenous variables X. So Y=S(Y,X). We now solve that system to get the reduced form system of equations R, with all the Y variables on the left hand side, and all the X variables on the right hand side. So Y=R(X).
And let's just assume that we know for sure that our model is the absolute truth about how the Y variables are determined, and that we know with absolute certainty the exact numerical values of all the parameters in R. So if we know X, the model can tell us Y. So far so good.
How does this model give us any help whatsoever to forecast future values of Y?
Most models that economists learn about don’t have any of the elements that allow them to do forecasting, at least not in the statistical sense. Nick’s right, as there’s no way to predict what the future value of a given variable would be in the framework of an economic model, unless you “guesstimate” what the values of the dependent variables will be in the future.
And that does not even take into account that most economic variables are endogenous – in Econoenglish, every variable affects all the others (including itself). If that’s the case, you might as well guesstimate the whole lot and as long as your guesstimates are internally consistent and look plausible, you’ll look like a decent economist. A lot of the criticisms about the ETP and NEM numbers are less about their accuracy (since nobody can know how accurate they are until 2020), but more about their internal consistency.
But to get back to the problem with forecasting, especially over longer periods, the essential thing to remember is this: while what you most likely see from most published forecasts is a single number, what any forecasting model actually does is generate a distribution of probabilities. In other words, it really should be a forecast range, not a forecast number. And the longer the period you’re trying to forecast, the greater the forecast uncertainty i.e. the bigger the forecast range.
To illustrate what I mean, let’s take a simple 1-lag autoregressive forecast model for Malaysian GDP. Everyone’s interested in whether we’ll achieve the goal of becoming a High Income Economy by 2020, so let’s see what happens.
The forecast model takes the form:
Ln(Y) = β0D1 + β1D2 + β2D3 + β3D4 + γAR(1)
where the D variables are quarterly seasonal dummies, and the AR(1) term models the error term as a 1-lag autoregressive function of its past values (i.e. εt = αεt-1 + θ)
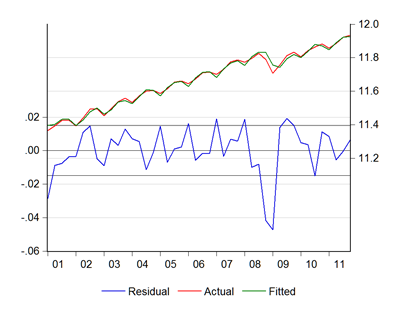
Using quarterly real GDP data from 2000:1 to 2011:4, this results in:
Ln(Y) = 14.43*D1 + 14.45*D2 + 14.48*D3 + 14.47*D4 + [AR(1)=0.996]
…and graphically:
…which looks like a close representation of the actual numbers. Forecasting forward, this is what I get:
I’ve departed from my usual practice and included two standard error lines on each side of the point forecast instead of just one.
The space between the inner two lines (bracketing the central line) covers the range of values that have a 2/3 probability of being realised – 66.6% of the time, these are the numbers that will actually occur (always assuming of course that the distribution is Z-normal). The space between the one standard error and two standard error lines on both sides covers another 30% or so – in total, the space covered by the lines will describe GDP 95% of the time.
In statistical terminology, this is your 95% confidence interval – you’re confident that 95% of the time, this is where GDP will end up.
But taking a closer look, these are the generated growth rates across the intervening years between now and 2020:
| +2se | +1se | Point | -1se | -2se | |
| 2012 | 9.9% | 7.3% | 4.7% | 2.1% | -0.5% |
| 2013 | 7.6% | 6.1% | 4.4% | 2.7% | 0.9% |
| 2014 | 6.5% | 5.5% | 4.4% | 3.2% | 1.8% |
| 2015 | 6.1% | 5.3% | 4.4% | 3.3% | 2.2% |
| 2016 | 5.8% | 5.1% | 4.3% | 3.4% | 2.4% |
| 2017 | 5.6% | 5.0% | 4.3% | 3.5% | 2.5% |
| 2018 | 5.5% | 4.9% | 4.2% | 3.5% | 2.6% |
| 2019 | 5.3% | 4.8% | 4.2% | 3.5% | 2.6% |
| 2020 | 5.2% | 4.7% | 4.2% | 3.5% | 2.6% |
Notice that the range estimates are pretty wide – from over 10% for 2012-2013 (a result of using the actual 2011 figure as the base year), before settling down to about 2.6% between the high estimate and the low estimate in 2020. Even though this suggests a seeming narrowing of uncertainty, it’s a more a result of a linear projection of the standard errors. Here’s the estimates for the projected marginal increase in real GDP over the 8 years to 2020:
| +2se | +1se | Point | -1se | -2se | |
| 2020 | 74.6% | 60.6% | 46.6% | 32.6% | 18.6% |
The point of this whole exercise is less about the accuracy of the forecast (I’m not going to pretend that it is), but to illustrate the uncertainty involved.
The forecast range, where you’re 95% sure GDP will end up, is incredibly wide. On the other hand, if you want to work towards a single number, or a narrower range of numbers, you’re sacrificing certainty – the narrower your range, the greater the uncertainty i.e. the lower the probability of hitting the target (and that includes overshooting it).
What happens if I include structural components in the model (consumption and investment for example)? That actually makes things a little worse – each component will have its own level of uncertainty, and the requirement of internal consistency means that any forecast based on structural components will be that much harder to achieve. In the context of what the NEM model describes numerically, having more target variables that have to be met substantially reduces the probability of any given outcome being achieved. And I’m not even going to bring up the problem of an evolving economic structure (i.e. the relationships between the variables will change over time).
In forecasting, simple models generally perform better (smaller standard errors). Structural models are better at analysing policy options, and are less useful for forecasting. Tweaking the numbers published in the ETP and NEM for “accuracy” might be a lot of fun, but in the end, it’s not a terribly fruitful exercise.
There’s this desire for pseudo-accuracy in today’s society – we measure athletic contests like swimming and sprinting in 100ths of seconds; computing components are judged on millisecond responses; yet people are still the same biological analog machines we have been for centuries. And economies are nothing more than an aggregation of many, many of these machines, all doing their own thing.




The basic question is what is ETP's actual target?Is it 1.7 trillion nominal gni in 2020 which translates to 8.8% nominal growth per annum or is it RM48k per capita i.e abt 7.5% growth?Surely fixing the goalpost or the "true north" is not too difficult.
ReplyDeleteIt also begets the question that if EPP(which is not the whole economy creates 800 bil of GNI its negative growth outside the 131 EPPs.
Thus way I see it ETP is just one huge confusion.
It wld be more realistic n correct if they focus on policy i.e NEM,SRIs,.
Whats ur view!
The basic question is what is ETP's actual target?Is it 1.7 trillion nominal gni in 2020 which translates to 8.8% nominal growth per annum or is it RM48k per capita i.e abt 7.5% growth?Surely fixing the goalpost or the "true north" is not too difficult.
ReplyDeleteIt also begets the question that if EPP(which is not the whole economy creates 800 bil of GNI its negative growth outside the 131 EPPs.
Thus way I see it ETP is just one huge confusion.
It wld be more realistic n correct if they focus on policy i.e NEM,SRIs,.
Whats ur view!
Hi Hishamh,
ReplyDeleteJust wondering if you are familiar with how the i-banks, like Goldman Sachs, or Morgan Stanley do their forecasting? Do you think that they would apply such rules-based model forecasting, or perhaps use a more ad hoc model with a lot of tweaking here and there all the time? Just curious about the insights into how their "proprietary models" would actually work.
Also, let's say that model forecasting is not entirely useful, what would be an alternative method of forecasting?
In my view, I suppose at the end of the day, it depends on why you want to forecast. Because like you said, range forecasts are a lot more useful, in the sense, it would be very hard to tell the actual difference between a 5.0% growth or a 6.0% growth when it comes to what we experience on the ground level. To me, I'd like to know if the growth is going to be strong (5-6%) or weak (1-2%), or even a recession. That is probably more useful that just getting the "accuracy".
I think perhaps a bit more useful could be probability forecasts ala probit or logit models. For example, what is the probability of a recession say, 4 to 8 quarters from now?
Also, I am not too familiar with this, but perhaps there is some role in Bayesian statistics in forecasting. Because in "traditional" forecasting, the goal is to minimize standard error, but in Bayesian statistics, the goal is to "maximize likelihood". I mean I only know the tip of the iceberg about Bayesian forecasting, but I am exploring the role of model forecasting here.
@anon
ReplyDeleteThe ETP's true target is whatever gets us to high income status, which is defined by the World Bank. Since that's a matter of conjecture, I'm afraid the goalposts are going to keep changing right up to the last minute. It's the nature of the thing. Setting the target in stone won't change the end result.
@shihong
I have no idea how the investment banks come up with their forecasts. The only ones I know who use full scale models to forecast are the IMF and some of the major central banks (BNM doesn't).
I agree that accuracy isn't strictly necessary - you're not going to feel much of a difference between say 4.5% and 4.7% growth.
The probability-based forecasts have weaknesses because of the way they're constructed. You might want to explore Prof Hamilton's attempts at a recession measure at Econbrowser (link).
I'm not familiar with Bayesian methods either but I'm willing to give it a go (if I've got time). I ordered a number of books on forecasting but I'm waaay behind in my reading already.
I suspect a lot of investment houses use a combination of time series models and leading indicators, but this is just conjecture.
ReplyDeleteSome of those forecasting macro statistics just use Holt-Winters. Which is kind of cheating.
ReplyDeleteBut whatever makes the client happy.
Yeah, that is kinda cheating. Still it's better than just filling in the numbers.
ReplyDelete